比例时滞神经网络的全局多项式镇定性*
时间:2022-12-05 22:00:01 来源:雅意学习网 本文已影响 人 
王 宇,张诗茹,张渝佶,周立群
(天津师范大学数学科学学院,天津 300387)
近年来,神经网络被广泛应用于联想记忆、信号处理、人工智能、优化与控制等领域,这些应用大都要求神经网络是稳定的.但由于在网络运行中时滞的存在不可避免,因此学者一直致力于研究时滞神经网络的各种稳定性[1-3].神经网络在控制器的作用下达到稳定时,称该网络是可镇定的.镇定性也是一种稳定性,学者对时滞神经网络镇定性也进行了深入研究[4-8].
比例时滞是一种客观存在的无界时变时滞,其优点是系统可根据网络所允许的最大时滞去控制网络的运行时间.2011年,周立群[9]将比例时滞引入神经网络,构建了比例时滞神经网络(Proportional Delayed Neural Networks,PDNNs)模型.单调递增的比例时滞函数使得系统时滞具有可控性和可预测性,故许多学者对PDNNs的动力学,尤其是稳定性[10-18](包括镇定性[19-22])进行了众多研究.例如,张保生[1]利用Lyapunov泛函方法、Barbalat引理和平均值不等式讨论了时滞细胞神经网络的稳定性;
Zhou等[21]采用离散控制器,基于Lyapunov函数和LMI方法,获得了PDNNs的全局多项式镇定性和全局渐近镇定性判据.受文献[1,21]的启发,笔者拟针对一类PDNNs,采用状态反馈控制器,在激活函数有界且满足Lipschitz条件下,通过构造适当的Lyapunov泛函,并利用平均值不等式及其分析技巧,研究了该神经网络的全局多项式镇定性和全局渐近镇定性.
考虑如下PDNNs:
(1)

(H1) 在R上有界;
(H2) 满足Lipschitz条件,即存在常数li>0,使得
|fi(ξ)-fi(η)|≤li|ξ-η|ξ,η∈R,i=1,2,…,n.
为了使系统(1)镇定,取控制器ui(t)=-kixi(t),则系统(1)变为如下闭环系统:
(2)


其中α∈Z+.

注1全局多项式镇定性也是一种全局渐近镇定性,但其收敛速度比一般的全局渐近镇定性的收敛速度快.
引理1[1]若fi(·)(i=1,2,…,n)满足(H1)和(H2),则系统(2)一定存在平衡点.
引理2[1]若fi(·)(i=1,2,…,n)满足(H1)和(H2),则系统(2)的所有解在[0,+∞)上均有界.
引理3[1]若ai(i=1,2,…,n)为正数,则
(3)
令zi(t)=xi(et),则系统(1)和(2)分别变为
和
(4)

注3由定义1易知系统(2)与(4)具有相同的平衡点,即x*=z*.
定理1假设(H1)和(H2)成立,在状态反馈控制器ui(t)=-kixi(t)下,若存在α∈Z+和λ>0,使得
(5)

(6)

构造正定的Lyapunov泛函
其中α∈Z+,λ>0.沿系统(5)计算V(t)的上右Dini导数,由(H2),可得
(7)
根据平均值不等式(3),可得
(8)
(9)
将(8)和(9)式代入(7)式,可得
(10)
(10)式蕴含着V(t)≤V(lnt0),且
(11)

进而有
(12)


(13)

(14)
在(14)式中取σ=t,得到
于是由定义(2)可知系统(1)全局多项式镇定到它的平衡点x*.证毕.
定理2假设(H1)和(H2)成立,在控制器ui(t)=-kixi(t)作用下,若存在α-1∈Z+和λ>0,使得对于i,j=1,2,…,n,有


计算U(t)的右上Dini导数,可得
(15)
根据平均值不等式(3),可得
(16)
(17)
将(16)和(17)式代入(15)式,可得
(18)
于是U(t)≤U(lnt0),且
(19)

进而有

注4文献[1]中的系统为常时滞的,本研究中的系统为无界时滞的,时滞函数(1-qi)t依赖比例时滞因子qi的大小,因此就时滞函数而言,本研究推广了文献[1]的结果.另外,文献[1]中通过构造Lyapunov泛函、Barbalat引理和平均值不等式,得到的是常时滞神经网络的全局渐近稳定性,本研究中没有使用Barbalat引理,而是通过构造Lyapunov泛函和平均值不等式得到全局多项式镇定性,因此本研究所得结论更优.
定理1与定理2是对系统(1)进行非线性变换zi(t)=xi(et),在状态反馈控制器ui(t)=-kixi(t)作用下,得到系统(1)全局多项式镇定到它的平衡点x*.如果不进行该非线性变换,就只能得出系统(1)全局渐近镇定到它的平衡点x*.
定理3假设(H1)和(H2)成立,在控制器ui(t)=-kixi(t)作用下,若存在α∈Z+,使得
(20)

(21)
显然,平凡解y*=(0,0,…,0)T是系统(21)的平衡点.要证x*是系统(1)的全局渐近镇定的平衡点,只需证y*是系统(21)的全局渐近镇定的平衡点即可.
构造Lyapunov泛函
其中α∈Z+.沿系统(21)的解计算V(t)的上右Dini导数,根据平均值不等式(3)和(H2),可得
(22)
根据平均值不等式(3)和(22)式,可得
当y(t)=(y1(t),y2(t),…,yn(t))T≠0时,至少存在1个i,使得yi(t)≠0,于是由(20)式可得
因此D+V(t)<0.
当y(t)=(y1(t),y2(t),…,yn(t))T=0,y(qt)=(y1(q1t),y2(q2t),…,yn(qnt))T≠0时,有yi(t)=0(i=1,2,…,n),于是由(22)式的第1个等号关系,可得
当y(t)=y(qt)=0时,由(22)式的第1个等号关系,可得D+V(t)=0.
综上,当且仅当y(t)=y(qt)=0时,D+V(t)=0,其他情况都有D+V(t)<0.同时,当‖y(t)‖→+∞时,V(t)→+∞,即V(t)是径向无界的,因此系统(1)全局渐近镇定到它的平衡点x*.
定理4假设(H1)和(H2)成立,在控制器ui(t)=-kixi(t)作用下,若存在α-1∈Z+,使得对于i=1,2,…,n,有

证明构造Lyapunov泛函
其余证明过程类似定理2和定理3.证毕.
注5定理1~4的条件都依赖于比例时滞因子qi(i=1,2,…,n),因此本研究所得结果均是时滞相关的,能很好地反映出比例时滞因子对系统镇定性的影响.
注6在系统(1)中,当qj=1(j=1,2,…,n)时,本研究所得到结果仍然适用.
例1考虑如下二维比例时滞神经网络:
(23)

图1 无控制器时系统(23)的时间响应曲线Fig. 1 Time Response Curves of System(23)Without Control

情况1当控制器ui(t)=0(i=1,2)时,系统(23)的从不同初值初始的时间响应曲线如图1所示.由图1可以看出,此时系统(23)是不稳定的.
情况2控制器ui(t)=-kixi(t)(k1=1.5,k2=2),e1=2,e2=2.5,取α=2,当i=1,2时,通过计算可得
这满足定理3的条件,因此由定理3可以判断系统(23)全局渐近镇定到它的平衡点(0,0)T.
情况3在情况2的条件下,取λ=1,α=2,当i=1,2时,通过计算可得
由定理1可知,系统(23)的平衡点(0,0)T是全局多项式镇定的.
系统(23)的相图和时间响应曲线分别如图2,3所示.由图2,3可以看出,此时系统(23)是稳定的.

图2 系统(23)的相图Fig. 2 Phase Trajectory of System(23)

图3 系统(23)的时间响应曲线Fig. 3 Time Response Curves of System(23)
例2考虑如下二维比例时滞神经网络:
(24)

情况1当控制器ui(t)=0(i=1,2)时,系统(24)的从(0,1)T初始的相图和时间相应曲线分别如图4,5所示.由图4,5可以看出,此时系统(24)是不稳定的.

图4 无控制器时系统(24)的相图Fig. 4 Phase Trajectory of System(24)Without Control

图5 无控制器时系统(24)的时间响应曲线Fig. 5 Time Response Curves of System(24)Without Control
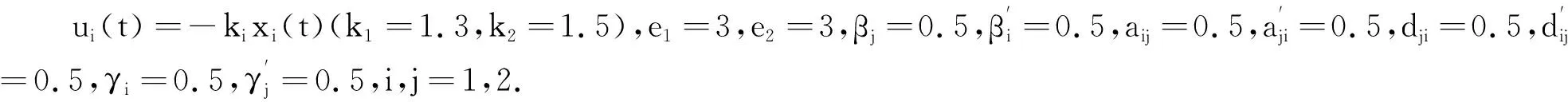
由定理4可知,系统(24)的平衡点(0,0)T是全局渐近镇定的.
情况3在情况2的条件下,取λ=1,α=2,当i=1,2时,通过计算可得
由定理2可知,系统(24)的平衡点(0,0)T是全局多项式镇定的.
系统(24)的相图和时间响应曲线分别如图6,7所示.由图6,7可以看出,此时系统(24)是稳定的.

图6 系统(24)的相图Fig. 6 Phase Trajectory of System(24)

图7 系统(24)的时间响应曲线Fig. 7 Time Response Curves of System(24)
综上,对于系统(23)和(24),在控制器ui(t)(i=1,2,…,n)作用下,分别应用定理3和定理4,可得它们平衡点的全局渐近镇定性,分别应用定理1和2,可得它们平衡点的全局多项式镇定性.根据注1,全局多项式镇定性收敛速度快于渐近镇定性,这说明定理1和定理2优于定理3和定理4.
研究了一类比例时滞神经网络的全局多项式镇定性,在状态反馈控制器作用下,通过构造适当的Lyapunov泛函,运用平均值不等式及其分析技巧,获得了保证系统时滞依赖的全局多项式镇定和渐近镇定的充分条件,并通过数值算例检验所得准则的有效性.本研究结果获得了相较全局多项式稳定性、全局渐近稳定性更优的结果,不足之处在于无法控制系统收敛到平衡点的速度.下一步笔者考虑如何让系统收敛的速度可控且尽量加快.
猜你喜欢 时滞平衡点全局 基于改进空间通道信息的全局烟雾注意网络北京航空航天大学学报(2022年8期)2022-08-31领导者的全局观中国医院院长(2022年13期)2022-08-15时滞非线性复杂动态网络的牵引自适应控制同步性廊坊师范学院学报(自然科学版)(2021年2期)2021-09-10Lotka—Volterra竞争扩散系统连接边界平衡点和正平衡点行波解的存在性教育教学论坛(2019年27期)2019-07-30落子山东,意在全局金桥(2018年4期)2018-09-26不确定时滞系统的整体控制稳定性分析智富时代(2018年4期)2018-07-10不确定时滞系统的整体控制稳定性分析智富时代(2018年4期)2018-07-10中立型随机时滞微分方程的离散反馈镇定上海师范大学学报·自然科学版(2018年3期)2018-05-14环境保护投资与经济发展的关系现代经济信息(2016年8期)2016-12-26建筑业营改增下适用税率的选择现代企业文化·理论版(2016年19期)2016-12-21







